Instantaneous phase
The notions of Instantaneous Phase and Instantaneous Frequency are important concepts in Signal Processing that occur in the context of the representation and analysis of time-varying signals. In signal processing, the instantaneous phase (or "local phase" or simply "phase") of a complex-valued function 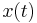 is the real-valued function:
is the real-valued function:
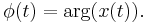 (see arg function)
(see arg function)
And for a real-valued signal 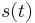 it is determined from the signal's analytic representation,
it is determined from the signal's analytic representation, 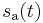 :
:
When 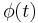 is constrained to an interval such as
is constrained to an interval such as ![(-\pi, \pi]\,](/2012-wikipedia_en_all_nopic_01_2012/I/169d31f8c073e17a7eceafd2dee2aede.png) or
or 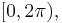 it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument
it is called the wrapped phase. Otherwise it is called unwrapped, which is a continuous function of argument 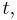 assuming
assuming 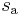 is a continuous function of
is a continuous function of 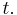 Unless otherwise indicated, the continuous form should be inferred.
Unless otherwise indicated, the continuous form should be inferred.
Contents |
Examples
- Example 1:
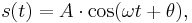 where
where 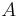 and
and 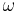 are positive values.
are positive values.
- Example 2:
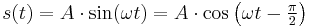
For both of these sinusoidal examples, the local maxima of 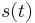 correspond to
correspond to
for integer values of 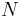 . Similarly, the local minima correspond to
. Similarly, the local minima correspond to
and the maximum rates of change correspond to
For signals that are approximately sinusoidal, these properties can be used, e.g., in image processing and computer vision, to detect points that are close to edges or lines, and also to measure the position of these points with sub-pixel accuracy.
Instantaneous frequency
In general, the instantaneous angular frequency is defined as
- and the instantaneous frequency (Hz) is:
-
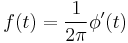 .
.
Conversely, the unwrapped phase can be represented in terms of an instantaneous frequency. When it is actually constructed/derived this way, this process is called phase unwrapping:
A similar definition can be used to describe phase as a function of frequency. In this case, the complex notation of phase generates values from ±180 degrees, but for unwrapped phase, an additional 360 degrees of phase must be added when the phase moves from +180 to -180 degrees. In this way, the phase will accumulate to any arbitrarily large value. Note from the definition that the phase function must exist for all frequency from f=0. In many cases, such as RF and Microwave measurements of cables or filters, the phase response is not measured continuously, but from some non-zero start frequency. In this case, phase unwrapping has ambiguities due to the lack of knowledge of phase response before the start frequency. In this case, it is common practice to assign the integral a value of zero for phase response before the start frequency. For devices such as cables, which have nearly constant phase vs frequency, this can give an error in the unwrapped phase response compared to the expected value as the phase before the start frequency is not included.
Complex representation
In some applications, such as averaging the values of phase at several moments of time, it may be useful to convert each value to a complex number, or vector representation:
This representation is similar to the wrapped phase representation in that it does not distinguish between multiples of 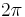 in the phase, but similar to the unwrapped phase representation since it is continuous. A vector-average phase can be obtained as the arg of the sum of the complex numbers.
in the phase, but similar to the unwrapped phase representation since it is continuous. A vector-average phase can be obtained as the arg of the sum of the complex numbers.
See also
References
- Cohen, Leon (1995). Time-Frequency Analysis. Prentice Hall.
- Granlund; Knutsson (1995). Signal Processing for Computer Vision. Kluwer Academic Publishers.
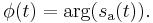
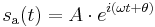
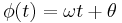
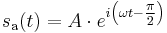
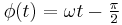
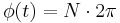
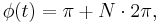
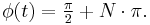
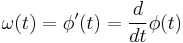
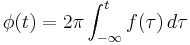
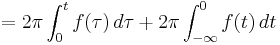
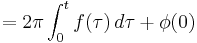
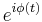
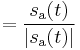
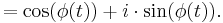 (
(